这是hcz写的最小生成树总结
最小生成树小结
Kruscal
思路
手动模拟
求该图最小生成树
此时最小边为1,且1和2节点不在同一棵树
可以连接
此时边数为1
图中Y代表选过的点或边,N代表排除掉不满足条件的边
此时最小边为3,且2和3节点不在同一棵树
可以连接
此时边数为2
此时最小边为4,但1和3节点在同一棵树
不可以连接
此时边数仍为2
此时最小边为5,且1和4节点不在同一棵树
可以连接
此时边数为3,达到n-1,如图便是该图的最小生成树
实际操作中
使用并查集合并
模版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 int gfa (int i) return fa[i] == i ? i : fa[i] = gfa (fa[i]); } struct zf { int a, b, c; }sz[11010 ]; bool cmp (zf x, zf y) return x.c < y.c; } for (int i=1 ;i<=10000 ;i++){ fa[i] = i; } int m=0 ; sz[++m].a = i; sz[m].b = j; sz[m].c = a; sort (sz+1 , sz+1 +m,cmp); int ans=0 ; int cnt = 0 ; for (int i=1 ;i<=m&&cnt< n-1 ;i++){ int x = gfa (sz[i].a); int y = gfa (sz[i].b); if (x!= y){ cnt ++; ans += sz[i].c; fa[x] = y; } } printf ("%d" , ans);
列题
模版题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 for (int i=1 ;i<=n-1 ;i++){ char a; cin >>a; int b; cin >> b; for (int j=1 ;j<=b;j++){ char c; cin >>c; int d; cin >> d; sz[++m].a = a - 'A' + 1 ; sz[m].b = c - 'A' + 1 ; sz[m].c = d; } }
思考题
nkoj极地网络
这道题重点在于思路部分,点的数量仅需\(P-S\) 条边
还有一个重点,在处理边时要运用勾股定理计算
\(\sqrt{(x_{1}-x_{2} )^{2}+
(y_{1}-y_{2} )^{2}}\)
代码重点部分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 for (int i=1 ;i<=p;i++){ for (int j=i+1 ;j<=p;j++){ a[++c].x=i; a[c].y=j; a[c].z=sqrt (1.0 *(bb[i]-bb[j])*(bb[i]-bb[j])+1.0 *(b[i]-b[j])*(b[i]-b[j])); if (i==j) a[c].z=INT_MAX; } } for (int i=1 ;i<=c;i++){ long long ta=fa (a[i].x),tb=fa (a[i].y); if (ta!=tb){ cnt++; ans=max (ans,a[i].z); f[ta]=tb; } if (cnt==p-s) break ; }
prim
思想
一开始树上只有一个节点
选择与树距离最近的一个不在树上的节点,加入树中
反复执行,直到所有点都加入树中
代码(LJ版)
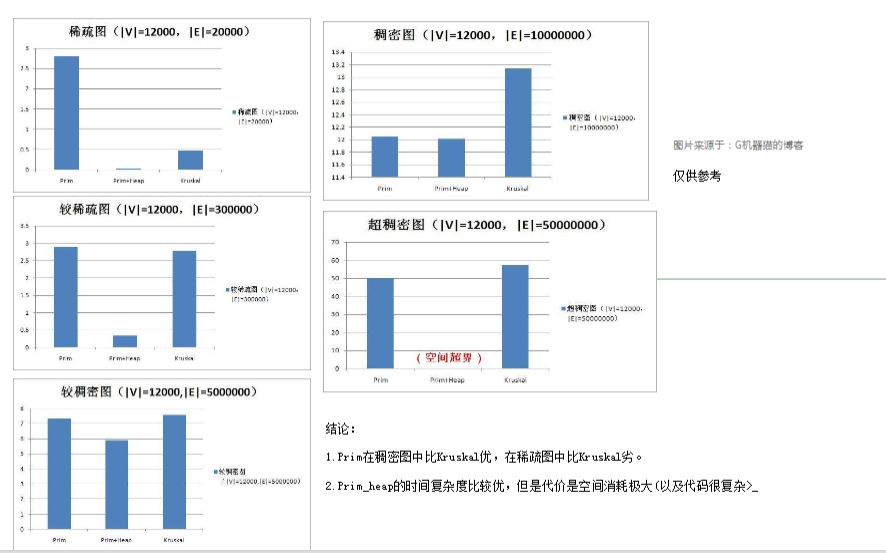
prim+堆在许多情况下比\(Kruscal\) 快
\(Kruscal\)
.png)
.png)
.png)
.png)
.png)