ST表，LCA，线段树 笔记

作者：\(hcz\)

ST表

基本原理

在求区间最值时，若一个大区间若能被两个小区间覆盖，那么大区间的最值等于两个小区间的最值。

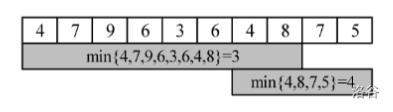
如图

步骤

1. 把数列按倍增分成小区间

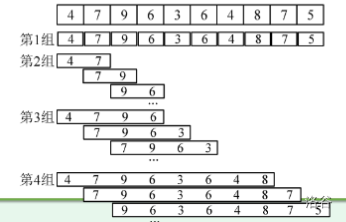
如图，直接明了

2. 查询任意区间的最值

把需查询区间 \([l, r]\) 分为两个区间，且两区间同属一组：

  • 以 \(L\) 为起点的小区间
  • 以 \(R\) 为终点的小区间

这两个小区间首尾相接覆盖 \([L, R]\)

实现

\(f[i][j]\) 表示从第 \(i\) 个位置开始，长度为 \(2^j\) 的区间的最大值。

预处理

\[ f[i][0] = a[i] \]

\[ f[i][j] = \max(f[i][j-1], f[i + 2^{j-1}][j-1]) \]

查询

查 \([l, r]\) 先找到最大的满足 \(2^j \le r - l + 1\) 的 \(j\)

\[ j = \lfloor \log_2(r - l + 1) \rfloor \]

区间最值为：

\[ \max(f[l][j], f[r - 2^j + 1][j]) \]

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for(int i=1; i<=n; i++) {
    cin >> f[i][0];
}

// 预处理
k = log2(n);
for(j:1--k){
    for(i:1--(n-(1 << j - 1)) ){
        f[i][j] = max(f[i][j-1], f[i+(1 << j - 1)][j-1]);
    }
    for(;i<=n;i++){
        f[i][j] = f[i][j-1];
    }
}

//查询
//查l--r的最值
int j = log2(r - l + 1);
int ans = max(f[l][j], f[r - (1 << j) + 1][j]);

例题

B - 【RMQ】奶牛探洞 | CQNK

十分典型的一道 RMQ 问题，计算最小值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int j=1;j<=log2(n);j++){
    for(i=1;i<=n-(1<<j-1);i++){
        f[i][j] = min(f[i][j-1], f[i+(1 << j - 1)][j-1]);
    }
    for(;i<=n;i++){
        f[i][j] = f[i][j-1];
    }
}
for(int i=1;i<=q;i++){
    int l, r;
    cin >> l >> r;
    int j = log2(r-l+1);
    printf("%lld\n", min(f[l][j], f[r - (1 << j)+1][j]));	
}

LCA

求最近公共祖先。

步骤

  • 求 \(u,v\) 的最近公共祖先
  • 调整 \(u,v\) 至同一高度

如果 \(\text{depth}[u] > \text{depth}[v]\)，将 \(u\) 向上跳 \(s = \text{depth}[u] - \text{depth}[v]\) 步，用倍增方式实现。

当 \(u,v\) 高度相同后，再“试着”继续上跳：

  • 设 \(k = \lfloor \log_2(\text{height}) \rfloor\)
  • 尝试跳 \(2^k\) 步，若 \(f[u][k] \ne f[v][k]\) 则跳
  • 尝试跳 \(2^{k-1}\) 步...
  • 直到跳 \(2^0\) 步

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void dfs(int u, int fa){
    for(int i=0; i<g[u].size(); i++){
        int v = g[u][i];
        if(v == fa) continue;
        d[v] = d[u]+1;
        anc[v][0] = u;
        dfs(v, u);	 
    }
}

int lca(int u, int v){
    if(d[u] < d[v]) swap(u, v);
    for(int i=log2(n); i>=0; i--){
        if(d[anc[u][i]] >= d[v]){
            u = anc[u][i];
        }
    }
    if(u == v) return u;
    for(int i=log2(n); i>=0; i--){
        if(anc[u][i] != anc[v][i]){
            u = anc[u][i];
            v = anc[v][i];
        }
    }
    return anc[u][0];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
for(int i=1; i<n; i++){
    // 输入u, v
    g[u].push_back(v);
    g[v].push_back(u);
    fq[v] = 1;
}
cin >> m; 
int s=1;
for(int i=1; i<=n; i++){
    if(!fq[i]){
        s = i;
        break;
    }
}
d[s] = 1;
dfs(s, 0);

for(int j=1; j<=log2(n); j++){
    for(int i=1; i<=n; i++){
        anc[i][j] = anc[anc[i][j-1]][j-1];
    }
}
while(m--){
    //输入u, v
    printf("%d\n", lca(u, v));
}

线段树

可以实现在需要区间修改时高效处理（最值/和/异或.......）

线段树是一种特殊的二叉树，它可以将一个线性的序列组织成一个树状结构，从而可以在对数的时间复杂度下访问序列上的任意一个区间并进行维护。

对于编号为 \(i\) 的节点 \(Tree[i]\)：

  • 父亲为 \(Tree[i / 2]\)
  • 左子树为 \(Tree[i*2]\)
  • 右子树为 \(Tree[i*2+1]\)

模板（区间修改与查询,这里以区间求和为例）

1
2
3
4
5
6
int sz[MAX_N];
struct node {
    int l, r;
    int val;
    int lazy;
} Tree[4 * MAX_N];

左右节点求和 

1
2
3
void pushup(int p) {
    Tree[p].val = Tree[2*p].val + Tree[2*p+1].val;
}
建树 
1
2
3
4
5
6
7
8
9
10
11
12
void MakeTree(int p, int x, int y) {
    Tree[p].l = x;
    Tree[p].r = y;
    if(x == y) {
        Tree[p].val = sz[x];
        return ;
    }
    int mid = (x+y) / 2;
    MakeTree(p << 1, x, mid);
    MakeTree(p << 1 | 1, mid+1, y);
    pushup(p);
}
懒标记 
1
2
3
4
void Maketag(int p, int len, int x) {
    Tree[p].lazy += x;
    Tree[p].val += len * x;
}
下放懒标记 
1
2
3
4
5
6
void pushdown(int p) {
    int M = (Tree[p].r + Tree[p].l) >> 1;
    Maketag(p << 1, M - Tree[p].l + 1, Tree[p].lazy);
    Maketag(p << 1 | 1, Tree[p].r - M, Tree[p].lazy);
    Tree[p].lazy = 0;
}
区间修改 
1
2
3
4
5
6
7
8
9
10
11
12
void add2(int p, int x, int y, int k) {
    if(Tree[p].l > y || Tree[p].r < x) return;
    if(x <= Tree[p].l && Tree[p].r <= y) {
        int len = Tree[p].r - Tree[p].l + 1;
        Maketag(p, len, k);
        return;
    }
    if(Tree[p].lazy) pushdown(p);
    add2(p << 1, x, y, k);
    add2(p << 1 | 1, x, y, k);
    pushup(p);
}
区间查询 
1
2
3
4
5
6
7
8
int getsum2(int p, int x, int y) {
    if(Tree[p].l > y || Tree[p].r < x) return 0;
    if(x <= Tree[p].l && Tree[p].r <= y) {
        return Tree[p].val;
    }
    if(Tree[p].lazy) pushdown(p);
    return getsum2(p << 1, x, y) + getsum2(p << 1 | 1, x, y);
}

动态开点

模板(这里以维护最大值为例)

1
2
3
4
5
6
int sz[MAX_N], tot=1;//tot是当前使用的点的个数
struct node{
    int l = -1, r = -1;
    int val;
    int lazy;
}Tree[MAX_N];

左右节点求最大 

1
2
3
void pushup(int p){
    Tree[p].val=max(Tree[Tree[p].l].val , Tree[Tree[p].r].val);//需要修改
}
懒标记 
1
2
3
4
void Maketag(int p, int x){
    Tree[p].lazy +=x;
    Tree[p].val += x;//重点修改
}
下传懒标记 
1
2
3
4
5
6
7
8
9
10
11
void pushdown(int p, int l, int r){
    if(Tree[p].l == -1)Tree[p].l = ++tot;//没有左儿子就“生”一个
    if(Tree[p].r == -1)Tree[p].r = ++tot;//没有右儿子就“生”一个
    if(Tree[p].val){
        // int M = (Tree[p].r+Tree[p].l )>> 1;
        Maketag(Tree[p].l, Tree[p].lazy);
        Maketag(Tree[p].r, Tree[p].lazy);
        Tree[p].lazy = 0;
    }
    
}
区间修改(同模版)

查询区间最大值 

1
2
3
4
int getsum2(int p, int l, int r, int x,int y){
    if(l > y || r <x) return -1e9;//重点初始化易错
    ......
}

附上例题 数列操作(加强版)

例题

题目 方法 易错点
a.数列操作 修改Maketag , pushup , getsum 初始化应该为1e9
b.涂色 val用来维护当前区间被涂色的数量
e.小白逛公园 用maxs 维护最大字段和 多个值的维护方式
F - 【USACO NOV08 GOLD】开关灯 通过异或来维护灯的开关,Tree[p].val维护的是亮着的灯的数量 当前亮 = 总共 - 之前亮
m.区间连续值 与e相似,可以将0直接赋值为-1e6,求出最大子段和即为答案 如果求出来小于0直接输出0
g.蒟蒻的数列 核心在于使用动态开点进行处理 题目中所求区间是\([a,b)\)

算法对比

算法 优点 缺点 时间复杂度（预处理/单次查询或修改）
ST表 预处理简单，查询速度快，适合静态数据 无法动态更新数据，预处理占用较多空间 \(O(n \log n)\) / \(O(1)\)
LCA 适用于树结构中的最近公共祖先问题，查询速度快 需要构建树结构，不适用于其他类型的查询 \(O(n \log n)\) / \(O(\log n)\)
线段树 支持动态更新和区间查询，功能强大 实现复杂，占用空间较大，预处理时间较长 \(O(n)\) / \(O(\log n)\)